Specific heat and thermal conductivity
![]()
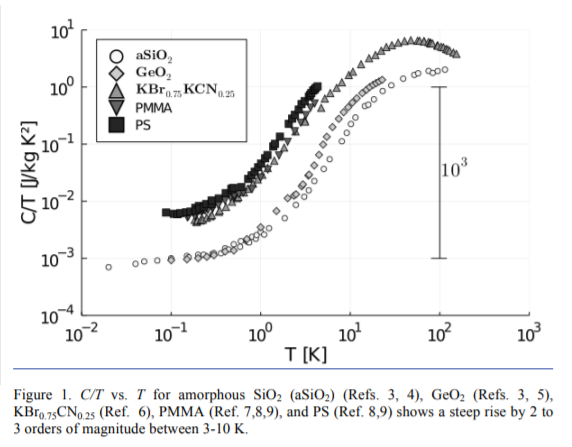
thesis The specific heat of pure and hydrogenated amorphous silicon
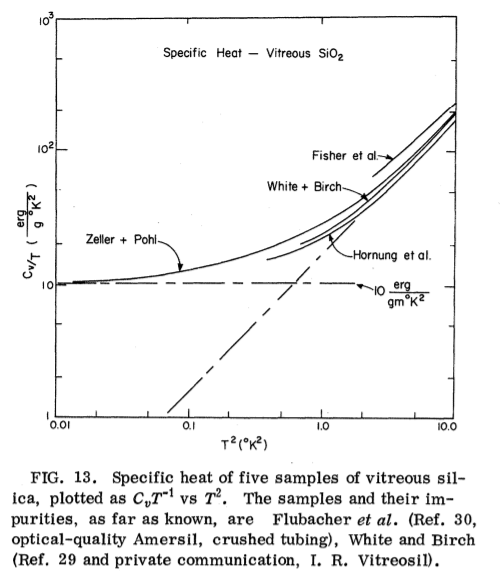
The specific heat of α-quartz follows the prediction of the Debye model at low temperatures but with a peak at 20K. This feature is due to non-propagating modes with zero group velocity that occur at the Brillouin zone boundaries where the phonon dispersioncurve is flat. The Debye model makes the assumption that the dispersion relation is linearwhich is suitable at very low energies (temperature). For higher temperatures one must usethe Born-von K ́arm ́an model which considers the full phonondispersion curve [29]
In a crystalline material the thermal conductivity can be divided into three regions: high temperatures where the phonon mean free pathℓis dominated by Umklappscattering, a peak whereℓis on the order of the impurity concentration or the sample dimension, and a low temperature region where the phonon population decreases as T3
Gopal - specific heat
It was noticed by *Birch and Clark (1940), and by Kittel (1948) that in glasses κ(T ) at T >20K *could be interpreted as the specific heat C(T)/V multiplied by a temperature-independent diffusivity D¯ of order a 2ωD/3 where a is an interatomic distance. In the phonon-gas
model, this would correspond to ℓ ≈ a, too small to justify use of the model. The success of this observation implies that the dominant normal modes in a glass are of the D variety, not P because P implies ℓ ≫ a, and not L because L implies D = 0 until anharmonic corrections are added which make D depend on T . This successful (and we believe, essentially correct) interpretation lost favor
after Anderson localization was understood, because a misconception arose that the P/D boundary (which certainly lies low in the sp
more specific heat